limx (x^2 y^2)
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/07 00:30:38
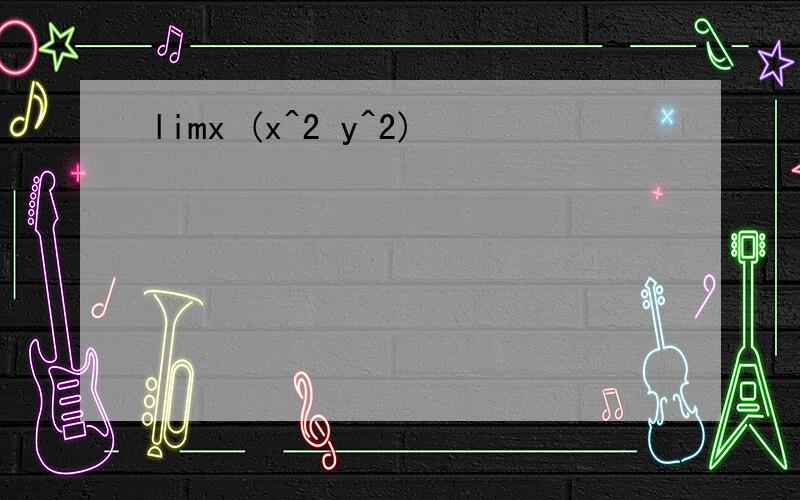
/>因为lim【x→1】2x+3=2×1+3=5lim【x→1】(x-1)/(2x+3)=(1-1)/(2×1+3)=0所以lim【x→1】(2x+3)/(x-1)=∞答案:∞
limx[ln(2x+1)-ln(2x)]=limx[ln(2x+1)/2x]=limln[1+1/2x]^x=limln[1+1/2x]^(2x.1/2)=limlne^(1/2)=1/2
limx→0[(x-sinx)/x²](0/0型)=limx→0[(1-cosx)/2x](0/0型)=limx→0(1/2)sinx=0.
先取对数原式化为lim(x-->0)ln[(x+e^2x-1)+1]/x=lim(x-->0)[e^2x-1+x]/x=lim(x-->0)e^2x-1/x+lim(x-->0)x/x=3所以原极限就
lim(4x²+5)/(x-2)=21/0+=+∞x→2+lim(4x²+5)/(x-2)=21/0-=-∞x→2-
limX趋近无穷x^2-1/2x^2-x=分子分母同除以x²,得limX趋近无穷(1-1/x²)/(2-1/x)=limX趋近无穷1/2=1/2
极限穷大时,认为极限不存在,这里暂时表述为极限是无穷大.
limx→∞(1+1/2x)^3x+2=limx→∞(1+1/2x)^2x*(3x+2)/(2x)=e^limx→∞(3x+2)/(2x)=e^(3/2)
我想楼主应该是想问这个吧:(1+1/x)^(3x+2)(+2是在指数的括号里),我就照这个答了,因为2加载外面没什么算的意义.整理一下式子,{(1+1/x)^x]^3}*(1+1/x)^2,可以看出,
limx/ln(1+x²)[分子分母都趋向于0]x→0=lim1/[2x/1+x²][运用罗毕达法则,分子分母分别各自求导了一次]x→0=lim(1+x²)/2x[分子趋
limx→0x^2/(x-1)=limx→0[(x^2-1)+1]/(x-1)=limx→0[(x-1)(x+1)+1]/(x-1)=limx→0(x+2)=2
你的思路不对,应该看做∞*0,接着就可以换成0/0的形式,就可以用落必达法则了.
lim1000x/(1+x^2)=lim(1000/x)/(1/x^2+1)=0.
先取自然对数limx->0ln(sinx/x)^(1/x^2)=limx->0(lnsinx-lnx)/x^2(这是0/0型,运用洛必达法则)=limx->0(cosx/sinx-1/x)/2x=li
直接将x=2y=0代入其中,得ln(2+e*0)/根号2*2+0*2)=ln3/2
上下乘√(x²+2x)+x=(x²+2x-x²)/[√(x²+2x)+x]=2x/[√(x²+2x)+x]上下除以x=2/[√(1+2/x)+1]2/
再问:感谢再答:懂了就好再问:limxcotxx如今于0求极限?
lim(x→0)sin3x/2x=lim(x→0)(sin3x/3x)*(3/2)=lim(3x→0)(sin3x/3x)*(3/2)lim(x→0)sinx/x=1=3/2
limx趋于0根号下(x^2-2x+5)=lim根号(0-0+5)=根号5再问:总感觉等于2倍根号2,当x为-1时就是2倍根号2,比根号五大啊。。。。
1.上下同乘e^-x2.lim(x→0)(x-arcsinx)/x^3 (0/0,洛必达法则)=lim(x→0)[1-1/√(1+x^2)]/(3x^2)(通分)=lim(x→0)[√(1+x^2)-