lim(x 0 y 0 ) x^2y (x^3 y^3)

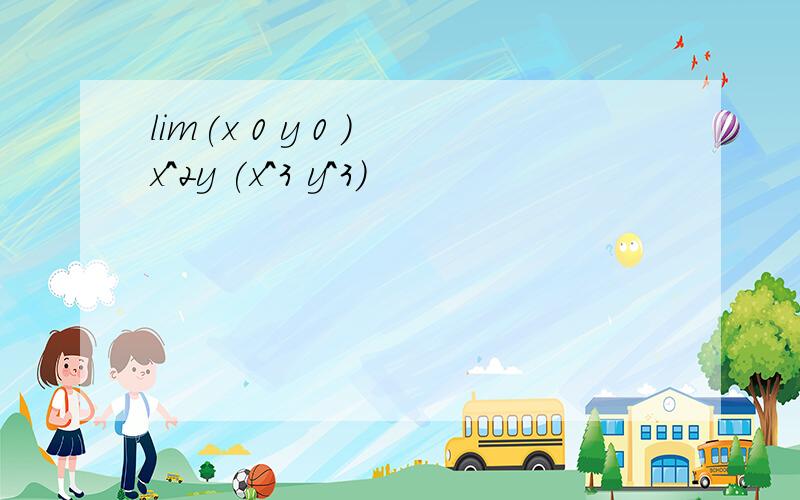
令：x=rcosθ,y=rsinθlim[(x,y)->(0,0)]((x^3)+(x^2)y+x(y^2)+(y^3))/((x^2)-xy+(y^2))=lim[(x,y)->(0,0)](r^3

方程两边对x求导得4x+2yy'=0即y'=-2x/y所以P点处k=-2x0/y0又过P(x0,y0)所以y-y0=k(x-x0)整理得2x0x+y0y=1（2）设A(x1,y1),B(x2,y2)则

极限不存在设y=kx^2代入得到：lim((x^2)y+x^5)/(x^4+x^6+2(x^3)y+y^2))(x,y)->(0,0)=lim(x->0)(kx^4+x^5)/(x^4+x^6+2kx

f(x,y)=(2-xy)/(x²+2y),这是一个初等函数,初等函数在定义域内均连续,而(0,1)显然是定义域内的点,因此连续,因此可直接算函数值就行了.lim(x,y)→(0,1)(2-

答案是0.首先,当0再问：�ܲ����������x=��sin��y=��cos��再答：�Ҳ����������˼�ǡ��ü�������������á�x=��sin��y=��cos�ȡ���

运用函数连续性,化成一元函数求极限x→0,y→2lim[ln(x+e^xy)/x]=x→0lim[ln(x+e^(2x)]/x【0/0型】=x→0lim[ln(1+(x+e^(2x)-1)]/x=x→

再问：请问您是不是有《大学数学习题册》的答案呀？可不可以发给我呀？我邮箱qf9292@163.com再答：真对不起，我没有。这题是我自己做出来的。

(1)令(x,y)沿y=kx趋近于（0,0）,则Lim（(x,y)→(0,0)）x+y/x-y=Lim（(x,y)→(0,0)）x+kx/x-kx=kk取不同值则极限也不同,所以极限不存在.（2）极限

同学：判定条件有两个；1：直线应该与圆有交点.就是原点到直线的距离小于或等于圆的半径!2：圆的半径应该是为正数!我自己还是没有做哦!你这样看看嘛.应该可以求解了!xo+yo=2a-1xo^2+y0^2

你这个题目存在很多问题,(lim)x/x-y是X除以X在减去Y呢,还是除以（X-Y）这个整体啊,细节问题啊,值得注意.如果我猜的没错的话,答案应该是1再问：(LIM)X→0Y→0再答：还是1

这个式子在(1,2)连续所以极限=(1+4)/2=5/2再问：可以写写计算的过程吗。再答：就是这个啊因为连续，所以可以直接代入

x0=3m1+1,y0=3m2+1,x0y0=(3m1+1)(3m2+1)=9m1m2+3m1+3m2+2=3(3m1m2+m1+m2)+2,所以x0y0∈N,不属于M

极限不存在吧x=ky时（k大于0）极限值与x=y^2时极限值不相等所以极限不存在对于多元函数要使得极限存在必须是从各个方向趋近极限值都一样.再问：答案极限为零主要是式子外面还有个X^2是那个式子的指数

若x+无穷=y+无穷[(x^2)/(2x^2)]^(x^2)=(1/2)^(x^2)=0

求极限lim(x,y)→(+∞,+∞)[(xy)/(x²+y²)]^(xy)[(xy)/(x+y)²]^(xy)≦[(xy)/(x²+y²)]^(xy

lim[x=y,x-->0](xy)^2/(x^2+y^2)^2=lim[x=y,x-->0]x^4/(4x^4)=1/4lim[y=2x,x-->0](xy)^2/(x^2+y^2)^2=lim[y

1.y=lim(x→0)(√1+xsinx-√cosx)/arcsin^2x=lim(x→0){[(sinx+cosx)/2√(1+xsinx)+sinx/2√cosx]}/[2arcsinx/√(1

是不是等于1?再问：😓😓😓😰就是不懂啊，不等于再答：请参考，不一定对

令y=kx则limsin(y×x^2+y^4)/(x^2+y^2)=limsin[kx^3+(kx)^4]/[(1+k^2)*x^2]分子用等价无穷小替换=lim[k+(k^4)*x]*(x^3)/[