dy dx=(x 1)^ (4y 1)^
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/11 00:26:46
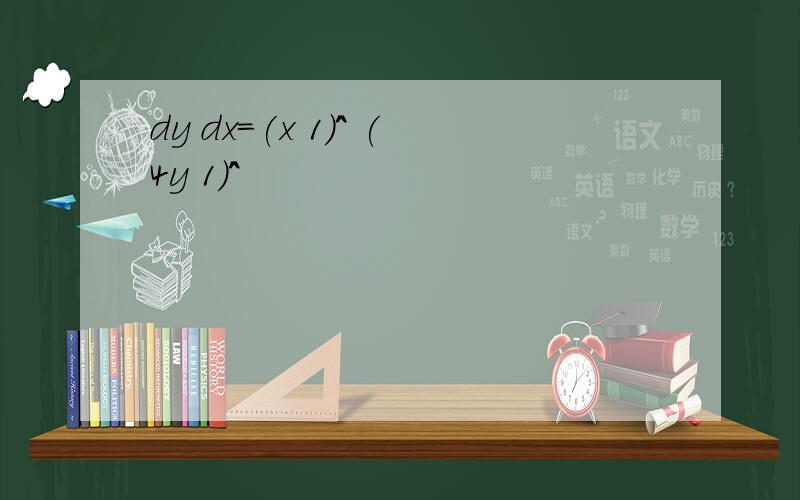
y=-4x+3画图像可以看出,斜率小于零是减函数所以x越大,y越小x1y2
因为x1所以-4x1>-4x2所以-4x1+3>-4x2+3所以y1>y2
∵y1=y2∴x1=-x2∴x1+x2=0
椭圆的方程是x2/4+y2/2=1吧,我就照这样做了(x2即x的平方)设PQ坐标分别为(x1,y1),(x2,y2)MF=a+ex=2+((根号2)/2)*1又因为等差数列得2MF=FP+FQ=(a+
首先你要知道斜率是什么设P1(x1,y1)P2(x2,y2)则斜率k=(y2-y1)/(x2-x1)①(这是定义)移项得y2-y1=k(x2-x1)可化为y-y1=k(x-x1)②将①代入②得y-y1
由题意可知A、B两点经过F(1,0)点,且直线斜率一定存在,设直线AB:y=k(x-1),(k>0),与椭圆方程联立,k²x²-(2k²+4)x+k²=0x1+
①x1>x2当x1>x2>0时,函数y=4/x当x>0时,y随x的增大而减小∴y1x1>x2时,函数y=4/x当x
这是不定方程组,因为未知数的数量(6)大于方程组数量(4),有无数组解.令X1=a,X2=b,则:由X1+Y2=3得Y2=3-a;由Y1+X2=1得Y1=1-b;由X1+Z2=6得Z2=6-a;由Z1
x1=2cosay1=4sina设那点是Q则A(2cosa+4sina,2cosa-4sina)x=2cosa+4sinay=2cosa-4sina所以x+y=4cosax-y=8sinasin&su
x1+x2=a+b再答:y1×y2=a×b再答:x1+x2+y1×y2=a+b+a×b
dydx要是等式才行吧.如果是的话,这句话就是求这个等式的根,用r表示x.
焦点(1,0),准线x=-1A到准线距离=x1-(-1)=x1+1B到准线距离=x2+1抛物线上的点到焦点和到准线距离相等所以AB=AF+BF=A到准线距离+B到准线距离=x1+1+x2+1=x1+x
2(x1-x2)-3(y1-y2)=0(y1-y2)/(x1-x2)=2/3=k即直线斜率所以y-y1=2/3(x-x1)3y-3y1=2x-2x13y=2x-(2x1-3y1)=2x-4即y=2x/
/>利用抛物线的定义即可抛物线x²=(1/4)y准线是y=-1/16,焦点F(0,1/16)利用抛物线的定义|AF|=y1+1/16,|BF|=y2+1/16∴|AB|=|AF|+|BF|=
首先考虑固定一点(x1,y1),求(x2,y2)使|x1-x2|+|y1-y2|最小.代入y2=6-2x2得|x1-x2|+|y1-6+2x2|=|x1-x2|+2|(y1/2-3)+x2|≥|x1-
addr=htonl(INADDR_ANY);default:return0;menu(仿照for(p=0;p
1)x1^2/4+y1^2/2=1,①x2^2/4+y2^2/2=1,②①-②,(x1+x2)(x1-x2)/4+(y1+y2)(y1-y2)/2=0,x1+x2=2,∴(y1-y2)/(x1-x2)