ax² (2-a)x 1-a≥0
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/11 17:36:54
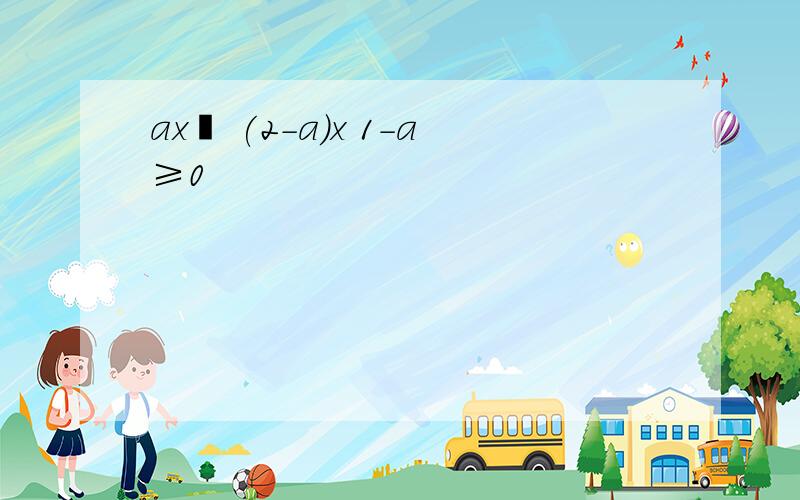
ax²-(3a+1)x+2(a+1)=0a-(a+1)1-2(ax-(a+1))(x-2)=0x=2x=(a+1)/a=1+1/aa≠0两个不相等的实数根(a+1)/a≠2a+1≠2aa≠1
f(x)=ax^2+2ax+4=a(x+1)^2-a+4∵x10∴f(x1)-f(x2)=[a(-x2+1)^2-a+4]-[a(x2+1)^2-a+4]=a(-x2+1+x2+1)(-x2+1-x2
由于f(x1)=f(x2)∴x1与x2是关于对称轴对称的两横坐标的值(因为x1,x2不等,说明两点异侧)∵x1,x2的对称轴为(x1+x2)/2∴f[(x1+x2)/2]就是其顶点的函数值了f[(x1
1)原式=√[(x1-x2)²]=√[(x1+x2)²-4x1x2]因为x1+x2=-b/a,x1x2=c/a所以原式=√(b²/a²-4c/a)2)原式=(x
对称轴x=-1(x1+x2)/2=(1-a)/20
依据求根公式得:x=[-b±√b^2-4ac]/2a∴|x1-x2|=[√b^2-4ac]/|a|x1^3+x2^3=(x1+x2)(x1^2+x2^2-x1x2)=-(b/a)[(x1+x2)^2-
x1+x2=1-a--->x1=1-a-x2f(x1)-f(x2)=a(x1²-x2²)+2a(x1-x2)+(4-4)=a(x1+x2)(x1-x2)+2a(x1-x2)=[a(
f(x)为偶函数x1+x2=0=>x1=-x2=>f(x1)=f(-x2)=f(x2)选B
这是根与系数的关系,也是韦达定理.两根之和x1+x2=-b/a两根之积x1x2=c/a
由抛物线经过点P(4,5),得到8a+m=5⑴再由三角形PAB的面积=10,得到(1/2)*(x2-x1)*5=10,得到x2-x1=4因为x2+x1=2,x2*x1=m/a所以(x2-x1)^2=(
就是0ap+bq+cr=x1^2008*(a*x1^2+b*x1+c)+x2^2008*(a*x2^2+b*x2+c)x1和x2是两个根,所以括号里的计算结果是0,和也是0.
f(x)=ax^2+2ax+4=a(x+1)^2-a+4因为x10所以f(x1)-f(x2)=[a(-x2+1)^2-a+4]-[a(x2+1)^2-a+4]=a(-x2+1+x2+1)(-x2+1-
f(x1)-f(x2)=ax1^2+2ax1+4-ax2^2-2ax2-4=a(x1^2-x2^2)+2a(x1-x2)=a(x1+x2)(x1-x2)+2a(x1-x2)=a(x1-x2)(x1+x
因为x1x2=c/a,x1+x2=-b/a(其中,a=1,b=-a,c=a^2-a+(1/4)),则,x1x2/(x1+x2)=a-1+(1/4a)∵Δ=a²-4(a²-a+1/4
首先你取个特殊的f——f(x)=x^2,代入计算,不难发现应该是填=f[(2x1+x2)/3]
ax^2+bx+c=0有两实根x1、x2,且|x1|4ac由于4a^2>b^2>4ac,所以a>cb^2>4ac>2bc,所以b>2c,所以c最小不妨设c=1,则a+1>b,所以a>=bb^2>4a>
ax^2+bx+c=0有两实根x1、x2,且|x1|4ac由于4a^2>b^2>4ac,所以a>cb^2>4ac>2bc,所以b>2c,所以c最小不妨设c=1,则a+1>b,所以a>=bb^2>4a>
答案错了,要求的值其实等于涵数的极值
将X1代入抛物线,得Y1=aX1²+2aX1+4将X2代入抛物线,得Y2=aX2²+2aX2+4Y1-Y2=a(X1²-X2²)+2a(X1-X2)=a(X1-
x1,x2是方程x^2-ax-6a=0的解韦达定理:x1+x2=a,x1*x2=-6a德尔塔=a^2+24a>=0,得a>=0或a