已知三棱柱abc-a1b1c1中,AB=BC=2,AC=2根号2

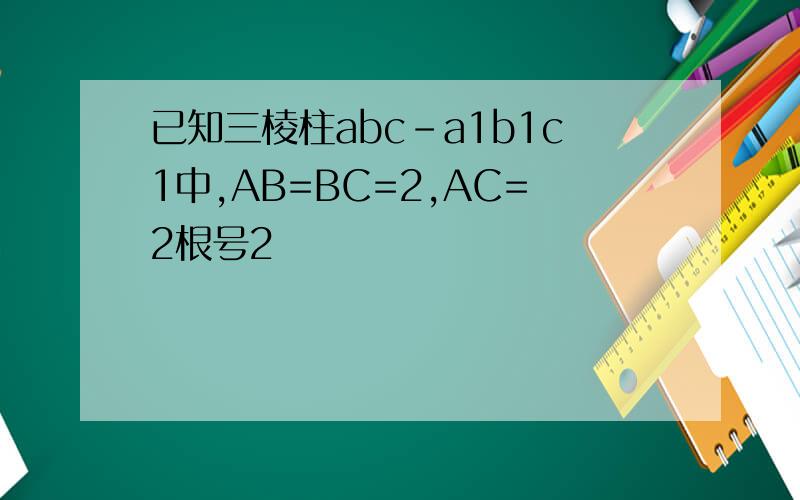
如图取AB的中点D，设侧棱长为a，因为AD=12，A1A=1，A1B1=2，∴Rt△A1AD≌Rt△B1A1A，∠AB1A1=∠AA1D，则A1D⊥AB1，又∵CD⊥AB，A1D∩CD=D∴AB1⊥面

设A1D∩AC1=E,∵AC1⊥平面A1BD,且A1D∈平面A1BD,∴AC1⊥A1D,在平面ACC1A1上,∵

图上不了,过A1点作AE⊥AC因为侧面A1ACC1垂直底面ABC所以A1E⊥BE,所以BE⊥AC,AE=EC=½a面A1ACC1⊥面A1EB,∠BA1C1=90°异面直线AC与BC1所成角即

很明显,高d^2=a-(√3a/3)^2d=√6a/3B点在则将三角形ABC的中心沿BC平行的方向移动a长度,设之在地面的投影为M则M到BC的距离=√3a/6BM^2=(√3a/6)^2+(a/2+a

（Ⅰ）证明：如图，已知AA1⊥平面ABC，BC⊂面ABC，∴AA1⊥BC，又已知AB⊥BC，且AB∩AA1=A，∴BC⊥平面AA1BB1，而BC⊂面A1BC，∴平面A1BC⊥面A1ABB1；（Ⅱ）过点

改用向量的方法,ef与A1B1没有直接联系必须借助其他的东西来证明

取AC的中点E，连接BE，C1E，∵正三棱柱ABC-A1B1C1中，∴BE⊥面ACC1A1，∴∠BC1E就是BC1与侧面ACC1A1所成的角，BC1＝3，BE=32，∴sinθ＝12，θ=30°．故答

（1）上下三角形的面积+三个长方形面积（2）添加辅助线：AC中点D与M点相连然后：显然BD是正三角形ABC的中垂线,MD是等腰三角形AMC的中垂线,这时观察Rt三角形MDB,发现二面角M-AB-C就是

（1）因为侧面A1ACC1垂直底面ABC,BC属于底面ABC,BC垂直AC,侧面A1ACC1交底面ABC=AC,所以BC垂直侧面A1ACC1,而直线AM在侧面A1ACC1上,所以直线AM垂直直线BC.

再问：我觉得应该是这样啊，但是长宁区2014一模卷的答案居然是具体数字！我觉得这非常的奇妙。。。再答：首先，你检查一下你上传题目时有没有漏掉一些内容，如果确认没有的话，就是它的题目有问题，题目只给出线

设棱长为6a,高为h由图知:CO=R=1又∵ CO2=2√3a ∴ (OO2)²=(CO)²－(CO2)² =1－12a²

我们把两个相同的正三棱柱合在一起,组成一个平行六面体ABDC-A1B1D1C1.则上下两个底面为菱形.连结C1D,则A1B‖C1D,所以,∠AC1D即为异面直线A1B与AC1所成的角.连结两底面的对角

你的图呢?没图怎么做?

过B作AC垂线交于D,连接C1D,角BC1D即为所求.tanBC1D=二分之根号三/二分之根号十七,再求反函数.

由题意，侧棱AA1长为底面△ABC内切圆的直径，∵三棱柱ABC-A1B1C1的底面是边长为3的正三角形，∴△ABC内切圆的半径为13•32•3=12，∴△ABC内切圆的直径为1，∴侧棱AA1长为1．故

题目没有给出这个三棱柱是不是正三棱柱,若是正三棱柱,则方法如下：第一个问题：过M作MN∥BC交CC1于N,令MN的中点为D.∵ABC－A1B1C1是正三棱柱,∴BM∥CN,又MN∥BC,∴BCNM是平

1、（1）连结矩形ABB1A1对角线AB1和A1B交于E,连结DE,平面ADB1∩平面BA1C1=DE,对角线相互平分,D是A1C1中点,E是AB1中点,DE是△A1C1B的中位线,DE‖BC1,DE

（1）三垂线定理证明（2）60°；因为C1C垂直于平面ABC所求角即角C1AC,又C1C=2√3,AC=2,所以角为60°

(1)连接AC1交A1M于N点∵角ACB=90度,角BAC=30度,BC=1AA1=√6M是CC1的中点∴CM=√6/2AC=√3=A1C1CC1=AA1=√6∴cotCAC1=cotC1MA1=√2