如图1-9,∠CDA=∠CBA,
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/11 17:53:13
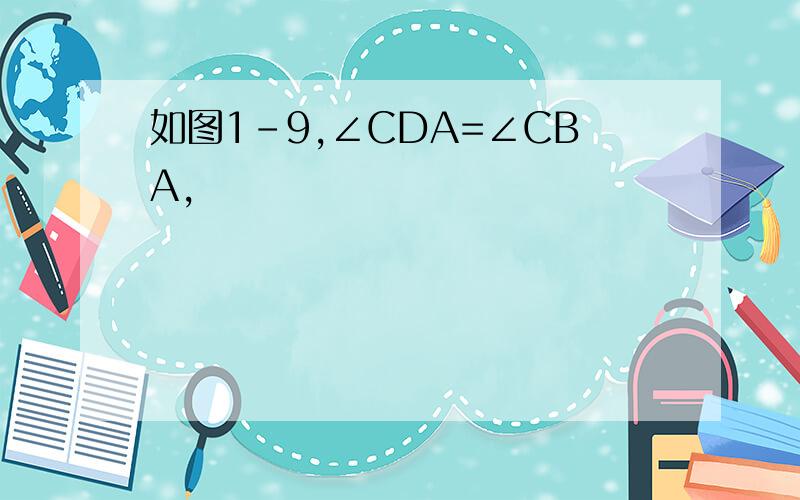
答:DE//FB理由:∵∠ADC=∠ABCDE平分∠CDABF平分∠CBA∴∠EDF=∠EBF∵AB//CD∴∠EDF+∠BED=180°(两直线平行,同旁内角互补)∴∠EBF+∠BED=180°∴D
先证明三角形ABC和BCD全等,理由是边角边:AB=CD,∠ABC=∠BCD,BC=BC.由此可得:BD=AC.又因为AB=BC,AD=AD(公共边)三边全等的三角形全等所以∠BAD=∠CDA再问:证
∠ADE=∠CDE=∠AED,又∠CDE=∠ABF,故∠AED=∠ABF,所以DE//FB
∵∠1+∠2=90°∴∠DEC=90°∴∠AED+∠BEC=90°∵CB⊥AB∴∠BEC+∠BCE=90°∴∠AED=∠BCE∵CE平分∠BCD,DE平分∠CDA∴∠ADE+∠BCE=90°又∵CB⊥
证明:在△ABC和△CDA中AB=CD(已知)∠BAC=∠DCA(已知)AC=CA(公共边)∴△ABC≌△CDA(SAS)
答:DE//FB理由:∵∠ADC=∠ABCDE平分∠CDABF平分∠CBA∴∠EDF=∠EBF∵AB//CD∴∠EDF+∠BED=180°(两直线平行,同旁内角互补)∴∠EBF+∠BED=180°∴D
小朋友,刚学全等吧.这题其实很简单,用SAS便可证明.在△ABD和△DCA中,AB=DC∠BAD=∠CDAAD=AD∴△ABD≌△DCA(SAS)加油哦!书山有路勤为径,学海无涯苦作舟.接下来你要学习
因为AB=DC,∠BAD=∠CDA.,AD是公共边所以△ABD≌△DCA.(根据边角边原则)
∵∠DAE=∠CAD-∠1∠BAD=∠CDA-∠B(三角形两个内角的和等于三角形第三个角的补角)又∵∠CAD=∠CDA,∠1=∠B∴∠DAE=∠BAD即AD平分∠BAE
因为∠1+∠2=90所以∠CED=90°,∠CEB+∠AED=90°又因为CB⊥AB所以∠B=∠BCE+∠CEB=90°又因为CE平分∠BCD所以∠2=∠BCE所以∠2+∠CEB=90°所以∠2=∠A
证明:(1)∵DE平分∠CDA,∴∠ADE=∠EDC,而∠ADE=∠AED,∴∠EDC=∠AED,∴AB∥CD;(2)∵BF平分∠CBA,∴∠ABF=12∠ABC,∵∠AED=∠ADE=12∠ADC,
你题目中的“CB平分AB”是一句废话,也是一句错话,删掉.求证的结论也是错的,应该是求证:E点平分线段AB.证明:取CD的中点F,连接EF由于角1+角2=90°所以:角DEC=90°,即△DEC是直角
∵CE平分∠BCD,DE平分∠CDA,∴∠1=12∠ADC,∠2=12∠BCD,∴∠1+∠2=12∠ADC+12∠BCD=12(∠ADC+∠BCD)=90°,∴∠ADC+∠BCD=180°,∴AD∥B
简单的问题,我初中就会了画了个图,你知道利用E,F点做辅助线,然后证明AB平行于CD就好
证明:∠ABC=∠CDA=90°,则:A,B,C,D在以AC为直径的同一个圆上.所以,∠1=∠2.(同弧所对的圆周角相等)(如果学过圆,这应该是最简单的方法了,用相似也可以,只是要多写几步了,如下:延
∵∠DAB+∠CDA=180°∴AB∥CD(同旁内角互补,两直线平行)∵∠ABC=∠1∴AD∥BC(同位角相等,两直线平行)再问:要因为什么,所以什么的。。再答:因为∠DAB+∠CDA=180°所以A
∠CDA=∠BAC由于∠CAD=∠B,所以∠CAD+∠BAD=∠B+∠BAD即∠BAC=∠B+∠BAD=∠CDA从而∠CDA=∠BAC
证明:∵CE平分∠BCD,DE平分∠CDA(已知)∴∠1+∠2=﹙∠BCD+∠CDA﹚/2(角平分线的性质)又∵∠1+∠2=90°(已知)∴∠=∠BCD+∠CDA=180°∴AD∥BC(同旁内角互补,
因为∠CDA=∠CBA(已知)又因为DE平分∠CDA,BF平分∠CBA(已知)所以∠ADE=∠CDE=∠CBF=∠ABF(等量代换)又因为∠ADE=∠AED(已知)所以∠AED=∠ABF(等量代换)所
证明:∵∠5=∠CDA(已知)∴AD∥BC(内错角相等两直线平行)∵∠5=∠ABC(已知)∴AB∥CD(同位角相等,两直线平行)∵∠2=∠3(已知)∴AB∥CD(内错角相等两直线平行)∵∠BAD+∠C