在△ABC中,∠c＝90°,∠b＝54°,∠ADC＝72

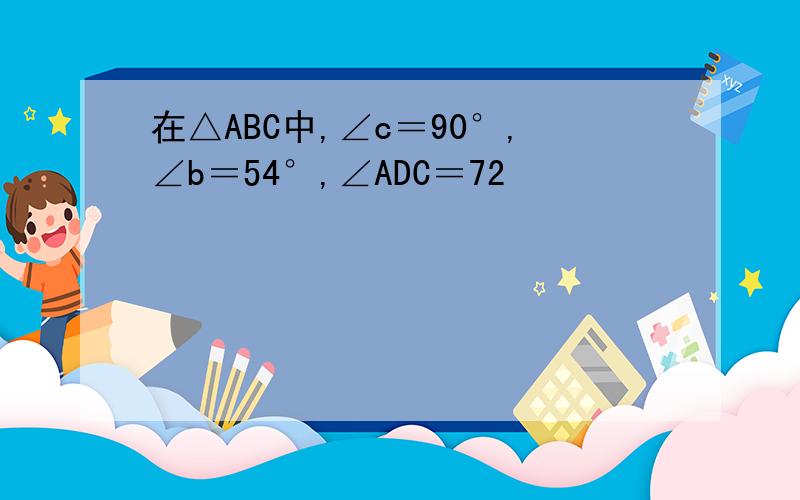
sinA的平方+sinB的平方=1sinA=cosBsinA=sin（90-B）

∵∠C=90°∴在Rt△ABC中，sinA=BCAB=25，设BC=2k，则AB=5k（k>0）在Rt△BCD中，∠BCD=90°，∠BDC=45°，∴∠CBD=∠BDC=45°．∴BC=CD=

令斜边上的高为h,则a*b＝c*h……①21/a＋21/b＝1……②√440/c＋√440/h＝1……③a²＋b²＝c²……④②式是由KE/BC＝AE/ABED/AC＝E

（1）tan角ABC=tan角ADC（2）2tan角ABC=tan角ADC（3）n角ABC=tan角ADC

∵在Rt△ABC中，∠C=90°，sinA=BCAB=45，∴AB=BCsinA=20÷45=25，∴AC=AB2−BC2=252−202=15，则△ABC的周长为25+15+20=60．故答案是：6

第一问：a=b=6√5,∠C=90°,则此为等腰直角三角形.c²=（a²+b²）,解得c=6√10,角A角B都是45°.第二问：a=2,c=3,∠C=90°,由c&sup

∵在△ABC中，∠C=90°，∴∠A+∠B=90°，∴cosB=sinA=35．

sinA=2/√5=2√5/5cosA=√5/5sinA+cosA=3√5/5

（1）AC=AB•sinB=20×sin45°=20×22=102，BC=AB•cosB=20×cos45°=20×22=102；（2）AC=AB•cosA=20×cos60°=20×12=10，BC

除以cos²A；tan²A-2tanA-3=0；0

（1）根据勾股定理可得：a=252−152=20；（2）∵△ABC为Rt△，∠A=60°，∴∠B=30°，∴c=2b，根据勾股定理可得：a2+b2=c2，即6+b2=（2b）2，解得b=2，则c=22

（1）∵∠C=90°，AB=c，∠A=30°，∴sinA=BCAB，cosA=ACAB，∴BC=c•sin30°=12c，AC=c•cos30°=32c；（2））∵∠C=90°，AB=c，∠A=45°

解题思路：在△ABC中，∠ABC＝【如果您无法查看，请先安装公式显示控件】本题可先根据cosB的值求出AB的长，然后通过证△ABD和△DCE相似，得出关于AB，CD，BD，CE的比例关系式，即可得出关

解题思路：：∵a+b=10∴（a+b）²=100a²+b²+2ab=100又∠C=90°∴a²+b²=c²=8²=64∴2ab=100-64=32ab=16∴½ab=8即S△ABC=8解题过程：解：∵

(1)勾股定理c=根号(4^2+8^2)=20根号2(2)即∠A=30c=2a勾股定理求出a=(10根号3)/3c=(20根号3)/3(3)即∠B=30b=0.5c=10a=10根号3

四边形ABCG是矩形证明：因为△ABC旋转60度后,E在AC上∴∠ACB=∠DCE=60°∴BE=EC=BC易证AE=EC∵∠AED=∠CED=90°,AE∶DE=CE∶DE=1∶√3∴∠EAG=60

（1）若已知a、∠A,则∠B=90°-∠A,b=a/tanA,c=a/sinA.（1）若已知c、∠B,则∠A=90°-∠B,a=c*cosB,b=c*sinB.（1）若已知b、∠A,则∠B=90°-∠

A'B'=ABA'B'⊥AB,理由如下：延长B'A'交AB于点D∵△CA'B'是由△ABC绕顶点C旋转的到的,∠ACB=90°∴△A'B'C'≌△ABC∴A'B'=AB∠B'=∠B∵∠A+∠B=90°

k≥3+2√2,当这个直角三角形等腰时,取得最小值,此时它的直角边长2+√2假设两直角边分别长x、y,则一定有x＞2,y＞2,不妨设x≥y,x-y=a≥0,则S△ABC=x+y-1=2x+a-1当x变