(y e^sinx)dx (x e^siny)dy
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/18 04:05:46
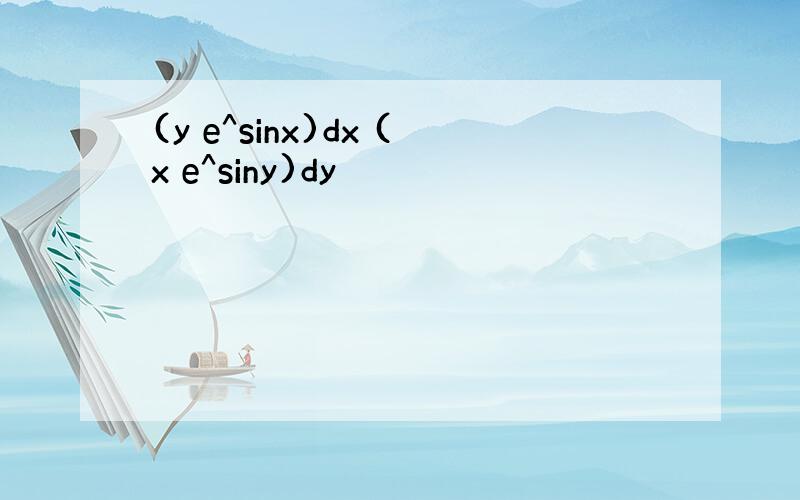
原式=(-1/2)*∫xd(e^(-2x))=(-1/2)*[xe^(-2x)-∫e^(-2x)dx=(-1/2)*xe^(-2x)+(1/2)*(-1/2)*e^(-2x)+c=(-1/2)*xe^
∫xe^xdx=∫xd(e^x)分部积分法:=xe^x-∫e^xdx=xe^x-e^x+c=(x-1)e^x+c有不懂欢迎追问再问:求抛物线y=x*2与直线y=1所围成的图形的面积~谢谢~再答:S=∫
(1)∫1/[x(x-1)]dx=∫[1/(x-1)-1/x]dx=ln|x-1|-ln|x|+C=ln|(x-1)/x|+C(2)∫cos2x/(sinx+cosx)dx=∫(cos²x-
原式=2∫xe^(x/2)d(x/2)=2∫xde^(x/2)=2xe^(x/2)-2∫e^(x/2)dx=2xe^(x/2)-4∫e^(x/2)d(x/2)=2xe^(x/2)-4e^(x/2)+C
我只告诉你怎么解得了,首先之方程式是非齐次方程,知道后就开始做第一步.先求出齐次方程的,即2y'-xe^y=0的函数式,比如y=cInx(C常数)这是其次的函数解,现在把c变成未知数u,那么y=uIn
∫xe^(-x)dx=-∫xd[e^(-x)]=-x·e^(-x)+∫e^(-x)dx=-x·e^(-x)-∫e^(-x)d(-x)=-x·e^(-x)-e^(-x)+C
前一个题目两边同时求导,也太简单了.第二个设y=x^5+x-1dy=5x^4+1,全域恒正,所以Y单调递增(R上的单调函数),由于X=0时Y=-1,x=1时y>0,所以,根据连续函数零值定理,在X=0
xe^y+ye^x=0直接对x求导x'*e^y+x*(e^y)'+y'*e^x+y*(e^x)'=0e^y+x*e^y*y'+y'*e^x+y*e^x=0e^y+(xe^y+e^x)*y'+ye^x=
分部积分法:∫xe^(-x)dx=-∫xd[e^(-x)]=-x·e^(-x)+∫e^(-x)dx=-x·e^(-x)-∫e^(-x)d(-x)=-x·e^(-x)-e^(-x)+C=-(x+1)e^
∫xe^(1/x)dx=-∫xe^(-x)d(-x)=-∫xde^(-x)=-(xe^(-x)-∫e^(-x)dx)=-xe^(-x)+∫e^(-x)dx=-xe^(-x)-∫e^(-x)d(-x)=
(e^y+xe^y*y')+(y'e^x+ye^x)=4y+4xy'(xe^y+e^x-4x)y'=4y-e^y-ye^xy'=(4y-e^y-ye^x)/(xe^y+e^x-4x)
∵xe^(2y)-ye^(2x)=1==>e^(2y)dx+2xe^(2y)dy-e^(2x)dy-2ye^(2x)dx=0(等式两端取微分)==>[2xe^(2y)-e^(2x)]dy=[2ye^(
1.令y=e^x,x=lny,dx=1/ydy.原式=∫lny/(y+1)^2dy分部积分:令u=lny,v'=1/(y+1)^2则∫lny/(y+1)^2dy=-lny/(y+1)+∫1/y(y+1
d(xe^y+ye^x)=0=d(xe^y)+d(ye^x)=xde^y+e^ydx+yde^x+e^xdy=xe^ydy+e^ydx+ye^xdx+e^xdy=(xe^y+e^x)dy+(e^y+y
其实就是隐函数求导,方程两边同时对x求导,y看做中间变量y'e^x+ye^x-e^y-(xe^y)y'=0所以dy/dx=y'=(e^y-ye^x)/(e^x-xe^y)
ye^x*log(ye)
分部积分∫xe^xdx=xe^x-∫e^xdx=xe^x-e^x